【図説】Excel(エクセル)の標準偏差の求め方｜グラフや関数の使い方を解説

更新日時 : 2024-03-29 11:56

データのバラつきを数値で判断するのに便利な標準偏差、業務で必要になるケースも多いです。

しかし、標準偏差を自分で計算しようとすると、平均値を求めて、分散を求めて、平方根にしてと、なかなか苦労することになります。

そんな標準偏差も、エクセルを使えば関数で簡単に求めることができます。また、エクセルなら標準偏差をグラフ化して、視覚的にさらに分かりやすくすることも可能です。

この記事では、標準偏差とは何かという基本から、標準偏差の計算方法、エクセルで関数を使って標準偏差を求める方法、標準偏差をグラフ化する方法を解説していきます。

目次

そもそも標準偏差とは？

標準偏差とは、データの中でバラつきや広がりがどれぐらいあるかを示す値になります。
標準偏差を使えば、そのデータの偏差が平均からどれぐらいあるかを確認することが可能です。

学校のテストの結果を見る時、平均を見れば、そのクラスの平均点は簡単に分かります。

ですが、平均は全体の点数を合計し、それを個数で割ったものにすぎないので、実際の点数状況とはかけ離れた印象になるケースもあります。

実際の点数が55点、45点、50点の平均点は50点です。

これは全て平均に近い数字ですが、点数が100点、30点、20点でも、平均は50点になります。

この例はサンプルが少なすぎますが、平均が分かったからといって、実際の数値が平均からどの程度離れているかは、確認してみないと分かりません。

標準偏差はこういった平均からでは分からない、平均から標準の偏差がどれぐらいあるかを確認できる値になります。

標準偏差を確認するにはまず平均値が必要になる

標準偏差は平均からどれぐらいバラつき・広がりがあるかを確認するものなので、まずは平均値を確認するのが必要になります。

平均の求め方はシンプルで、データを全て合計し、データの個数で割れば、平均値を知ることができます。

エクセルの場合はAVERAGE関数を使えば、簡単に平均を求めることができます。

標準偏差は分散を平方根にしたもの

標準偏差にはその前提として分散があります。分散もデータの広がり・バラつきを示す指標ですが、標準偏差とは単位が異なります。

また、分散は平均から数値が大きく離れてしまうことが多いので、数値から直観的に偏差を認識することが難しくなるのが問題です。分散を平方根にした標準偏差はこの問題を解決します。

分散の計算はそのまま標準偏差の計算につながるので、まずは計算式について確認していきましょう。とはいっても、標準偏差をエクセルで使う場合は自分で計算する必要は無いので、この計算を覚える努力はしなくても大丈夫です。

分散は下記の方法で、求めることができます。

• データの平均値を計算
• 各データと平均との偏差を算出
• 2乗した偏差の結果を合計
• 最後に2乗した偏差の合計を個数で割る

例として、エクセルで分散を求めたのが下の画像になります。

一応手順を解説していきますが、先述したようにエクセルで標準偏差を求める場合はこの計算を覚える必要はありません。

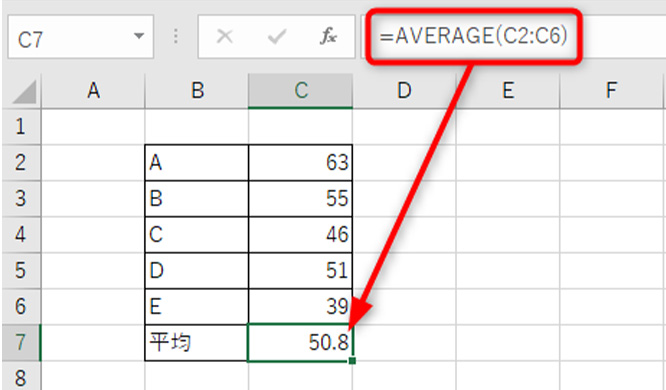
まずは、データの平均を求めます。

エクセルではAVERAGE関数を使えば、平均を簡単に求められます。例の場合だと、C8セルに、「=AVERAGE(C3:C7)」と入力しています。

平均が算出できたら、データから平均を引いて偏差を求めます。例では、D3セルに「=C3-$C$8」を入力し、下にオートフィルでコピーしています。
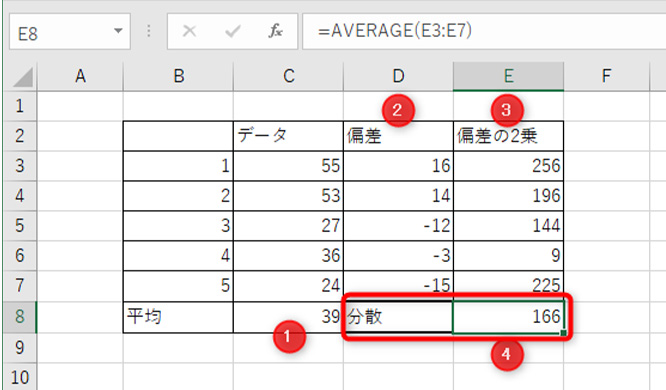
偏差を2乗します。例では、E3セルに「=D3^2」を入力し、下にオートフィルでコピーしています。
偏差の2乗から平均を求めて分散を取ります。例ではE8セルに「=AVERAGE(E3:E7)」を入力しています。

これで、分散は「166」であるというのが分かりました。

ただ、この「166」という数字は元データより桁が大きく、バラつきがどれぐらいあるかというのが判断しづらいです。

この分散を平方根にして、データのバラつきを分かりやすくしたのが標準偏差になります。

標準偏差の計算方法

エクセルで平方根を求める場合は、「=セル^(1/2)」という数式を使います。

先ほどの分散から標準偏差を求める場合は、H8セルに「=E8^(1/2)」と入力することになります。

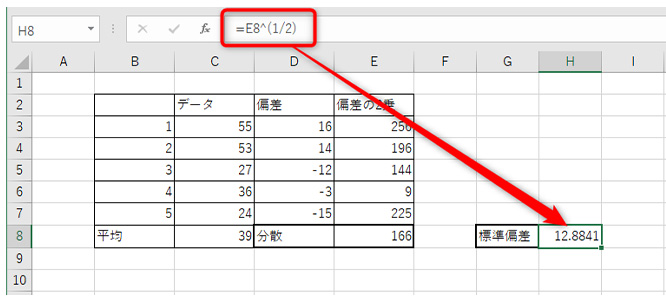
これで、このデータの標準偏差は「12.88」というのが分かりました。

このように、分散を計算して標準偏差を求めるというのは面倒な計算を伴います。ですが、エクセルの関数を使えばもっと簡単に標準偏差を求めることができます。

エクセルで標準偏差を求めるには関数を使う

エクセルで標準偏差を求めることができる関数は、「STDEV.P（スタンダードディービエーション・ピー）関数」と「STDEV.S（スタンダードディービエーション・エス）関数」の2つです。

STDEVが標準偏差の意味になり、その次のアルファベットの意味で、役割の異なる関数になります。

STDEV.P関数

STDEV.P関数は、データの母集団全てに対するバラつきを求める関数になります。

スタンダードディービエーション・ピーの「p」は「population（ポピュレーション）」の略で、母集団を意味しています。

学校のテストで、クラス30人分の全てをデータに含めて計算する、こういった場合に使うのが、STDEV.P関数です。

データを全て含んでいるので、STDEV.P関数では正確な標準偏差を得ることができます。

STDEV.S関数

STDEV.S関数は、母集団から無作為にデータを抜き出し、その標本からバラつきを求める関数になります。

スタンダードディービエーション・エスの「S」は、「sample（サンプル）」の略で、標本を意味しています。

日本全国の高校生のテストの標準偏差を求める際、全員のデータを集計して合計するというのは困難です。

そこで、全国の高校生から無作為に500人を抜き出し、そのデータを使って標準偏差を割り出す。
こういったケースで使用するのが、STDEV.S関数になります。

STDEV.S関数は全体から無作為にデータを抽出するため、この時点で必ずしも正確とはいえない結果が出てしまう可能性を含んでいます

STDEV.S関数はこの点を補正する機能を備えた関数なのですが、サンプルを抽出している以上、完璧なデータになるということはありません。

TDEV.S関数は全てのデータからバラつきを求めるSTDEV.P関数とは異なる結果が出てしまう可能性がある点に、注意してください。

STDEV.P関数とSTDEV.S関数の違い・使い分け

データの全てを使うのが、STDEV.P関数です。データから一部を抽出して計算するのが、STDEV.S関数になります。

全てのデータを合計して計算するなら、STDEV.P関数を使います。
一部のデータを抽出して使うなら、STDEV.S関数を使いましょう。

STDEV.P関数の使い方

実際にエクセルでSTDEV.P関数を使ってみます。

標準偏差を入力したいセルに、「＝STDEV.P(　」と入力します。

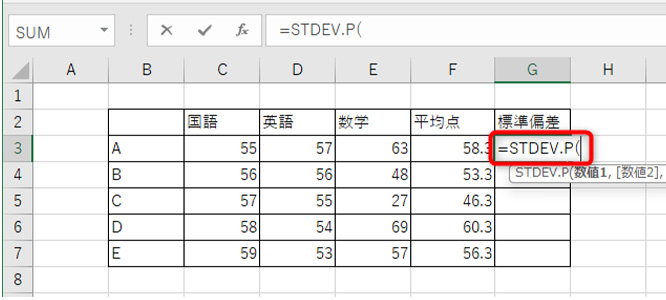
データを範囲選択。

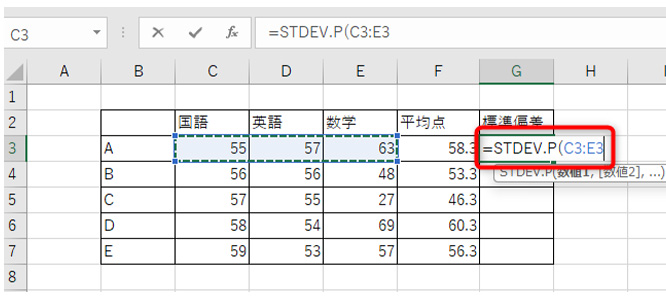
カッコで閉じて（もしくはTabキーで）、関数を確定します。

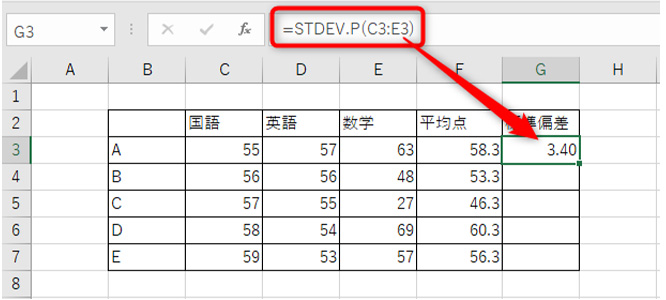
これで、標準偏差を求めることができます。

STDEV.P関数は範囲を選択するだけで標準偏差を求められるので、簡単に使える関数です。

STDEV.S関数の使い方

実際にエクセルでSTDEV. S関数を使ってみます。

標準偏差を入力したいセルに、「＝STDEV. S (　」と入力します。

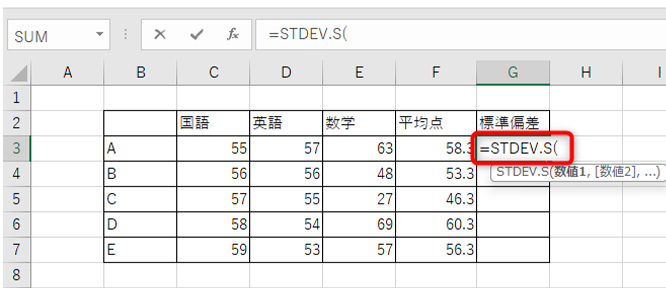
データを範囲選択。

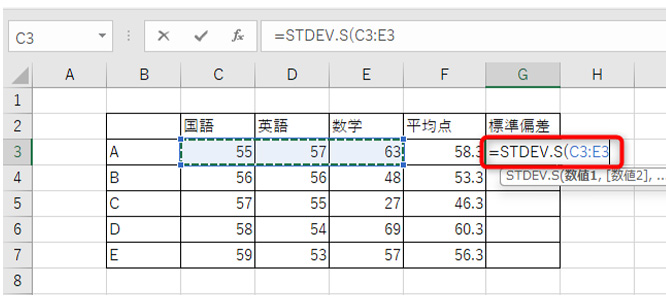
カッコで閉じて（もしくはTabキーで）、関数を確定します。

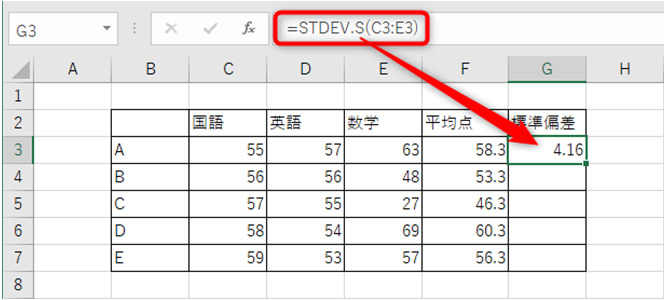
これで、標準偏差を求めることができます。

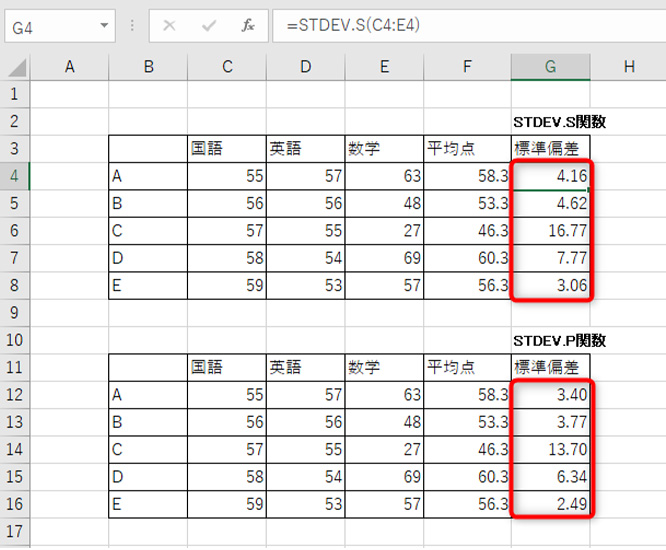
STDEV.P関数とSTDEV.S関数では結果が異なると解説したとおり、同じデータを使っても、標準偏差は異なった結果になっています。

エクセルの標準偏差は小数点何位まで書くのが正しい？

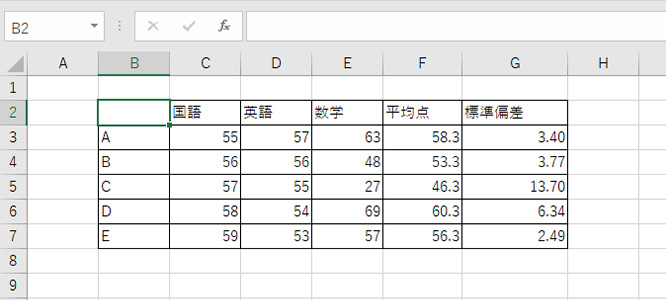
標準偏差は平方根なので、「4.163332」というように小数が長く続くことになります。これをそのまま表に入力した状態は見づらいので、小数を区切って整えると良いです。

正確さをどこまで求めるかなどによっても異なりますが、一般的に平均や標準偏差の少数は次のように整えるのが良いとされています。

エクセルで標準偏差の「2σ」・「3σ」を求める方法

標準偏差は「σ」であらわされるのですが、これを2倍したのが「2σ」です。標準偏差を3倍にしたのが、「3σ」になります。

一般的に標準偏差「σ」の値は平均値から68%が含まれる範囲とされています。「2σ」は95%の範囲、「3σ」は99.7%の範囲が該当すると言われています

エクセルで「2σ」・「3σ」を求める場合は、「σ」を2倍3倍するだけなので、簡単です。

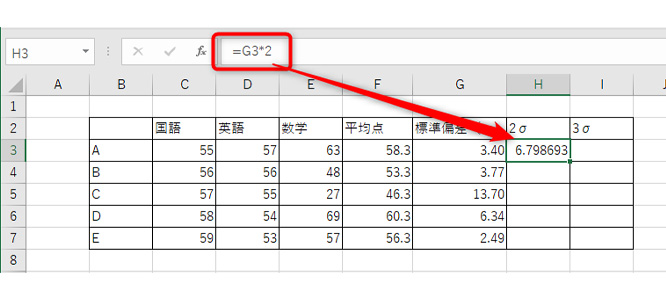
2σの場合は、標準偏差の「＝σが入力されたセル*2」としましょう。下画像の場合だと、「=G3*2」を入力しています。意味は参照したセルに2を掛ける、です。

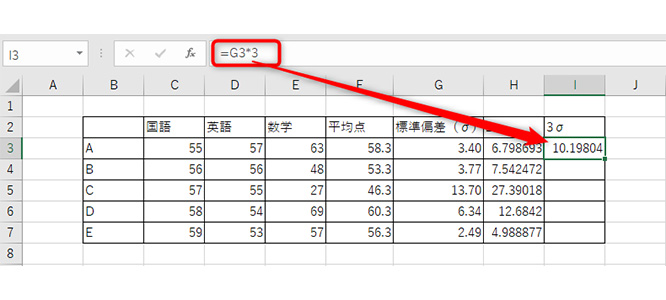
3σの場合は、標準偏差の「＝σが入力されたセル*3」です。下画像の場合だと、「=G3*3」と入力しています。意味は参照したセルに3を掛ける、です。

エクセルで標準偏差をグラフにする方法

標準偏差を数値化できると分かりやすいですが、標準偏差をグラフに応用すると、視覚的・直観的に分かるようになります。

標準偏差を散布図と棒グラフにする方法を解説していきます。

散布図

散布図は横軸と縦軸にそれぞれ別の量をとり、データが当てはまるところに点を打って示すグラフです。2つの量の関係を見るのに、非常に便利です。

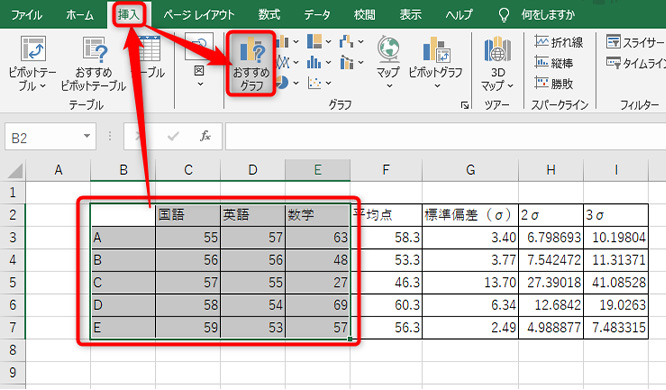
散布図にするには、データ範囲を選択し、「挿入タブ」から「おすすめグラフ」をクリックします。

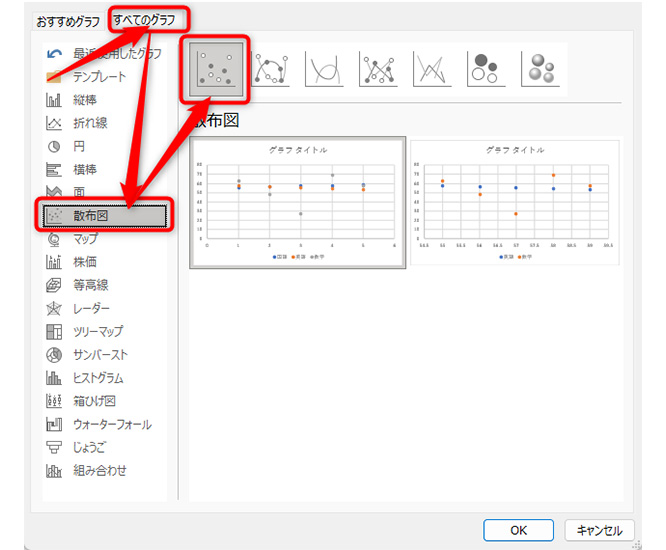
「すべてのグラフ」タブから散布図を選び、「OK」をクリック。

これで、散布図からデータのバラつきを確認できます。

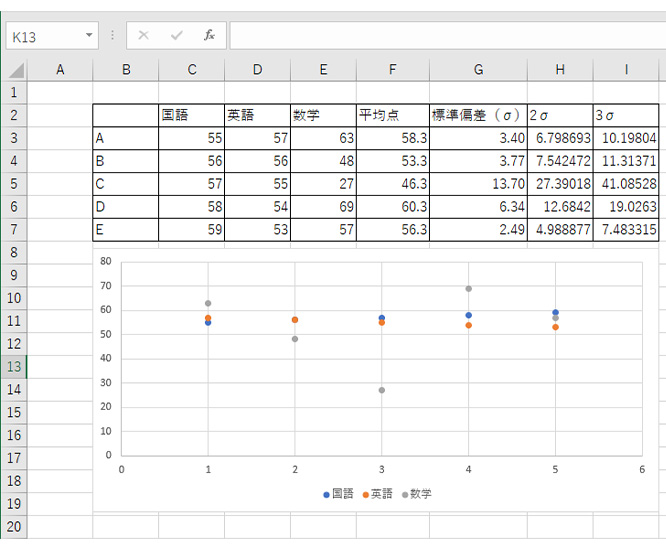
画像の場合だと、英語、国語はバラつきが低いけれど、数学に関してはバラつきが大きいというのが分かります。

棒グラフにエラーバーを付ける方法

棒グラフに標準偏差のエラーバーを付けると、バラつきを視覚的に確認できるようになります。

まずは、タイトルと平均値が入力されたセルを範囲選択します。

セル同士が離れている場合は、「Ctrl」キーを押しながら範囲を選択しましょう。
続けて「挿入」タブから、「おすすめグラフ」を選択。

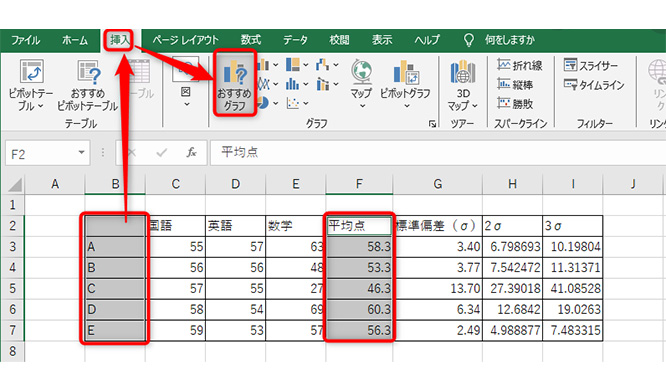
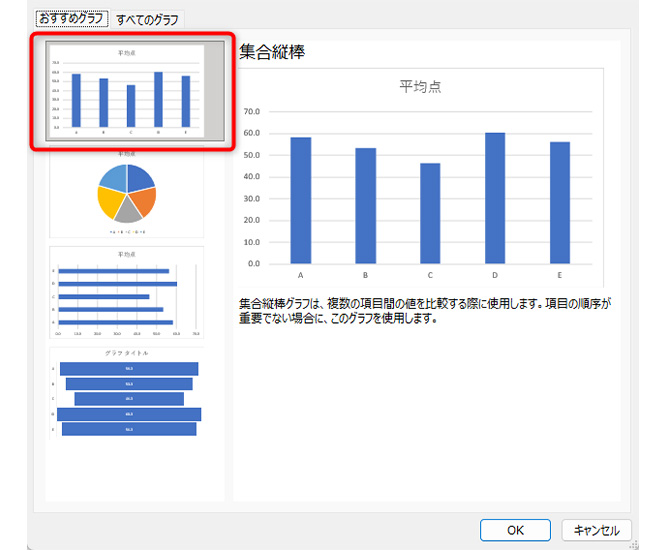
「集合縦棒」を選択して「OK」をクリックします。

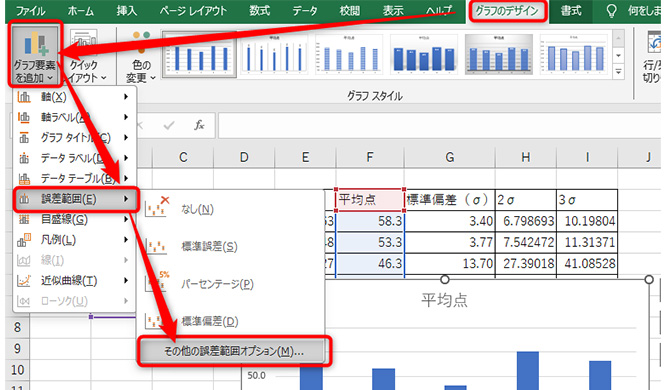
「グラフのデザイン」タブにある一番左側にある「グラフ要素を追加」から、「誤差範囲」に進み、「その他の誤差範囲オプション」をクリック。

ワークシート右に誤差範囲の書式設定が開くので、下部にある「ユーザー設定」にチェックを入れ、「値の指定」をクリックします。

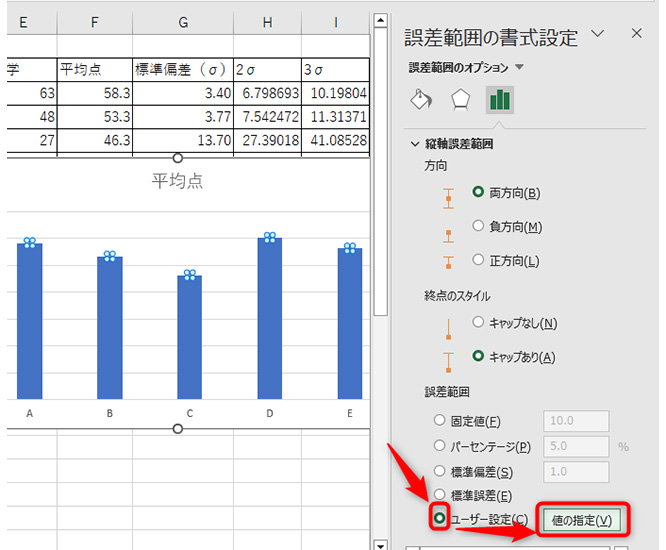
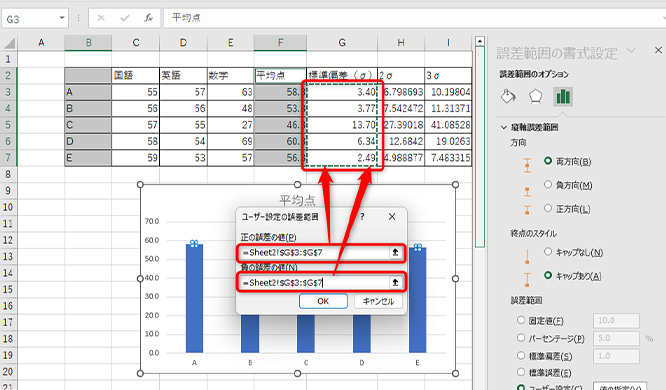
「正の誤差の値」「負の誤差の値」の範囲選択が開くので、それぞれに標準偏差が入力されたセルを範囲選択して、「OK」をクリックします。

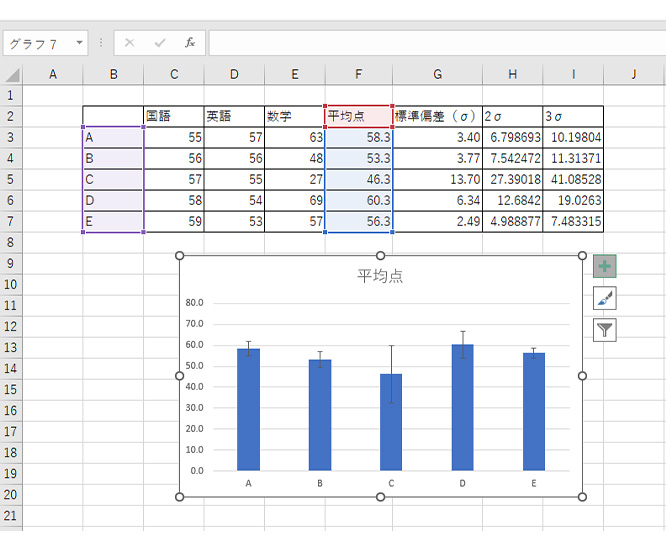
これで、エラーバー付の棒グラフ作成が完了です。

まとめ

エクセルを使えば面倒な標準偏差も簡単に求めることができます。

母集団を全てデータに含むなら、STDEV.P関数を使います。

母集団から標本を取り出して標準偏差を求める場合は、STDEV.S関数を使いましょう。

標準偏差を使えばデータのバラつきが簡単に分かります。

記事を参考にエクセルの標準偏差を使いこなしてみてください。

ノジマではパソコンのご購入や、パソコン操作のお困りごとなどのご相談を承っています。

気になることがありましたら、ノジマ店頭にてお気軽にご相談ください！

※ご相談内容によっては対応できかねる場合や、有料になる場合がございます。あらかじめご了承ください。